BAB II
KONSEP FUZZY LOGIC
Motivasi utama teori fuzzy logic adalah Memetakan sebuah ruang input kedalam ruang output dengan menggunakan IF-THEN rules.
Pemetaan dilakukan dalam suatu fuzzy interfence System (FIS), urutan rule bisasembarang.
FIS mengevaluasi semua rule secara simultam untuk menghasilkan kesimpulan.Oleh karenanya ,semua rule harus didefenisikan lebih dahulu sebelum kita membangun sebuah FIS yang igunakan untuk menginterpretasikan semua rule tersebut.
Konsep umum kronologi proses pembangunan FIS
Mekanisme dalam FIS dirangkum :
FIS adalah sebuah metode yang menginterpretasikan harga-harga dalam vector input menarik kesimpulan berdasar sekumpulan IF-THEN rules yang diberikan , dan kemudia menghasilkan vector output.
2.1 Fuzzy Set
Untuk memahami fuzzu logic, terlebih dahulu dimulai dengan memahami fuzzy set. Fuzzy set adalah sebuah himpunan di mana keanggotaan dari tiap elemennya tidak mempunyai batas yang jelas .Himpunan demikian sangat kontras dengan himpunan klasik.
Sebagai contoh : himpunan nama hari-hari dalam satu minggu dan himpunan selain nama-nama hari .Bisa dibuatkan dalam himpunan hari-hari dalam satu minggu atau pada himpunan hari-hari akhir minggu .
Dijelaskan didalamnya dari 7 hari dalam seminggu, jumat termasuk dalam Himpunan hari-hari akhir minggu selain sabtu dan minggu.
Cara kerja fuzzy logic hanya masalah generalisasi logika “ya-tidak” (Boolean). Misalkan ,dalam logika Boolean ,”benar” diberi bobot 1 dan “salah” diberi bobot 0, dalam fuzzy logic hal yang sama bias dilakukan dengan memboboti “benar”/”salah” dalam rentang 0 sampai 1.
Dialog ini memberikan contoh perlunya pemakaian fuzzy logic
A : apakah minggu adalah anggota himpunan hari akhir minggu?
B : 0.95 (ya,tidak sepenuhnya seperti hari sabtu terutama hari akhir minggu)
A : apakah sabtu adalah anggota himpunan hari akhir minggu ?
B : 1 (ya)
A : apakah selasa adalah anggota himpunan hari akhir minggu ?
B : 0(tidak)
A : apakah jumat adalah anggota himpunan hari akhir minggu?
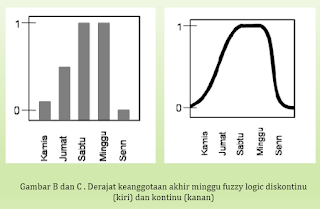
B : 0.8 (ya sebagian besar dan tidak sepanjang hari)2.2 Fuzzy Keanggotaan
Kurva pada gambar sebelumnya merupakan sebuah fungsi yg memetakan ruang input (waktu dalam seminggu) menjadi bobot atau derajat “akhir minggu” atau lebih sering disebut membership function (fungsi keanggotaan).
Fungsi keanggotaan mendefenisikan bagaimana tiap titik dalam ruang input dipetajam menjadi bobot atau derajat keanggotaan antara 0 dan 1.
Dalam teori himpunan,ruang input juga dikenal sebagai universe of discourse.
Secara umum ,beberapa kesimpulan tentang himpunan dan fungsi keanggotaan fuzzy diberikan di bawah ini :
1. Fuzzy set menekankan konsep variable samar (vague or fuzzy variable) seperti hari minggu ,suhu panas,pelari cepat,dll
2. Fuzzy set mengijinkan keanggotaan parsial dari suatu himpunan seperti hari jumat yang dianggap sebagai hari akhir minggu namun dengan derajat di bawah 1.
3. Derajat keanggotaan fuzzy dalam fuzzy set berkisar antara 0 sampai 1.
4. Tiap fungsi keanggotan µ berasosiasi dengan sebuah fuzzy set tertentu dan memetakan suatu nilai input ke nilai derajat keanggotaan yang sesuai. Misalnya dalam kasus fuzzy set orang berbadan “tinggi” mempunyai fungsi keanggotaan sendiri, yaitu µtinggi yang berbeda dengan fungsi keanggotaan dari fuzzy set orang berbadan “rendah” yaitu µ rendah.
2.3 Boolean Logic dan Fuzzy Logic
Merupakan sebuah fakta bahwa dalam fuzzy logic bersifat lebih general daeripada Boolean logic. Dalam fuzzy logic ,jika variable fuzzy diset pada derajat maksimumnya, yaitu 1 atau minimumnya yaitu 0, maka akan berlaku Boolean logic (atau two-valued logic).
Misalkan ada dua fuzzy set,yaitu A dan B dan ada sebuah anggota himpunan x. Anggota himpunan x ini bisa dikelompokan dalam fuzzy set A dengan derajat keanggotaan µA(x) dan juga fuzzy set B dengan derajat keanggotaan µB(x) . Sekarang lihat jika operasi min dilakukan antara dua fuzzy set A dan B tersebut di notasikan dengan :
min(µA(x),µB(x)
Berdasarkan gambar diatas, dengan menggunakan fungsi min, max dan 1-A untuk menggantikan operator AND, OR, dan NOT, kita bisa menggunakan sembarang variabel fuzzy untuk melakukan operasi-operasi fuzzy logic yg ekivalen dengan AND, OR, dan NOT, bahkan bisa lebih general.
2.4 Operator tambahan FUZZY LOGIC
Pada pembahasan sebelumnya memilih korespondensi AND = min , OR = max , dan NOT = komplemen penambahan. Dalam fuzzy logic kita bisa berkreasi sendiri dalam mendefinisikan sendiri fungs-fungsi yang bisa menggantikan operasi AND,OR,NOT. Namun fungsi-fungsi buatan sendiri tersebut harus mengacu pada aturan-aturan umum operasi fuzzy logic .
2.5 IF-THEN rule
Fuzzy logic bekerja berdasar aturan-aturan yang dinyatakan dalam bentuk pernyataan IF-THEN. Sebuah aturan fuzzy berbentuk seperti berikut :
if x is A the y is B